How Greedy Mining Strategies Impact Blockchain Throughput and Profits

Table of Links

Abstract and I. Introduction

II. Background

III. Problem Definition

IV. DAG-Oriented Solutions

V. Game Theoretical Analysis

VI. Simulation Model

VII. Evaluation

VIII. Countermeasures

IX. Discussion and Future Work

X. Related Work

XI. Conclusion and References

VII. EVALUATION

We designed a few experiments with our simulator, which were aimed at investigating the relative profit of greedy miners and transaction collision rate (thus throughput) to investigate Hypothesis 1. In all experiments, honest miners followed the RTS, while greedy miners followed the greedy strategy. Unless stated otherwise, the block creation time was set to λ = 20s. However, we abstracted from τ of transactions and ensured

that the mempools of nodes were regularly filled (i.e., every 60s) by the same set of new transactions, while the number of transactions in the mempool was always sufficient to fully satisfy the block capacity that was set to 100 transactions. We set the size of mempool equal to 10000 transactions, and thus the ratio between these two values is similar to Bitcoin [20] in common situations. In all experiments, we executed multiple runs and consolidated their results; however, in all experiments with the simple topology, the spread was negligible, and therefore we do not depict it in graphs.

A. Experiment I

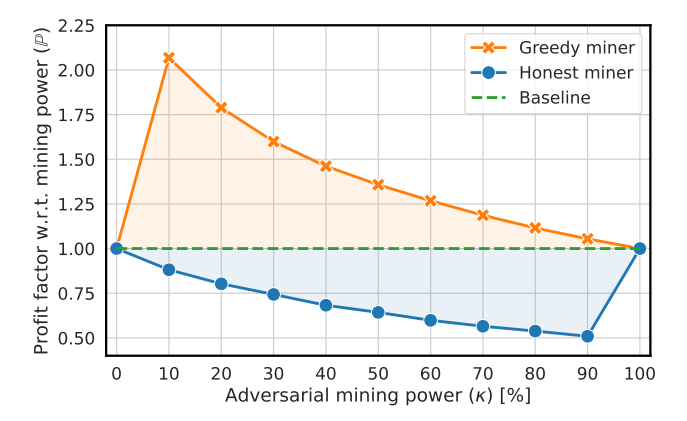
Goal. The goal of this experiment was to compare the relative profits earned by two miners/phenotypes in a network, corresponding to our game theoretical settings (see Sec. V). Thus, one miner was greedy and followed the greedy strategy, while the other one was honest and followed the RTS.

Methodology and Results. The ratio of total mining power between the two miners was varied with a granularity of 10%, and the network consisted of 10 miners, where only the two miners had assigned the mining power. Other miners acted as relays, emulating the maximal network delay of 5 hopes between the two miners in a duel. The relative profits of the miners were monitored in terms of their profit factor P w.r.t. their mining power.

We conducted 10 simulation runs and averaged their results (see Fig. 5). In all simulation runs, the greedy miner earned a profit disproportionately higher than her mining power, while the honest miner’s relative profit was negatively affected by the presence of the greedy miner. We can observe that P of greedy miner was indirectly proportional to her κ, which was caused by the exponential distribution of transaction fees that contributed more significantly to the higher P of a smaller miner. In sum, this experiment showed that the profit advantage of the greedy miner aligns with the conclusions from the game theoretical model, and its Scenario 5 (see Sec. V-B3) in particular, which represents the case of κ = 50%. Nevertheless, our results indicate that the greedy strategy is more profitable than the RTS for any non-zero κ.

B. Experiment II

Goal. The goal of this experiment was investigation of the relative profits of a few greedy miners following the greedy

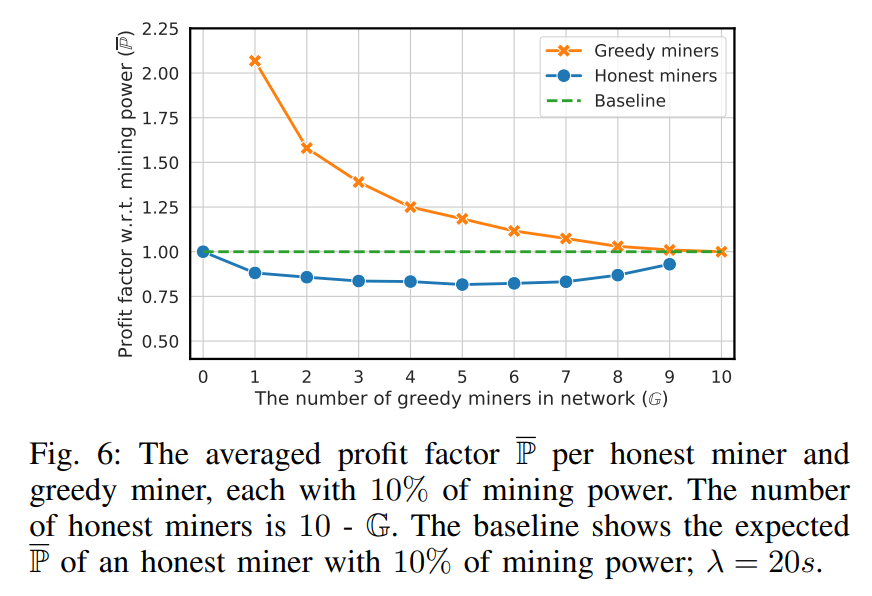
strategy in contrast to honest miners following the RTS.

This observation might be seen as beneficial for the protocol as it disincentivizes multiple miners to use the greedy transaction selection strategy, which would support the sequential equilibrium from Inclusive protocol [26]. However, as we mentioned in Sec. IV, the authors of the Inclusive protocol assume no cooperating players, which is unrealistic since miners can cooperate and create the pool to avoid collisions and thus maximize their profits (resulting in a similar outcome, as in Sec. VII-A). To further investigate the profits of mining pools, we performed another experiment as follows.

C. Experiment III

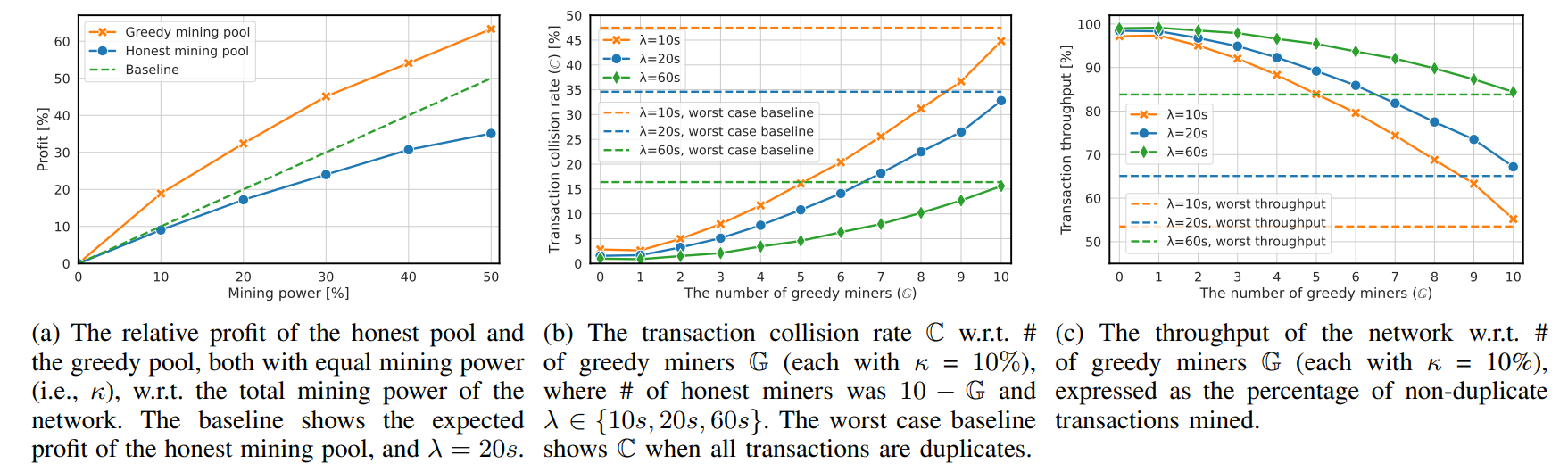
Goal. The goal of this experiment was to investigate the relative profit of the greedy mining pool depending on its κ versus the honest mining pool with the same mining power. It is equivalent to Scenario 5 of game theoretical analysis (see Sec. V-B3) although there is the honest rest of the network.

Methodology and Results. We experimented with 10 miners, and out of them, we choose one greedy miner and one honest miner, both having equal mining power, while the remaining miners in the network were honest and possessed the rest of the network’s mining power. In other words, we emulated a duel of the greedy mining pool versus the honest mining pool. We conducted 10 simulation runs and averaged their results (see Fig. 7a). The results demonstrate that the greedy pool’s relative earned profit grows proportionally to κ as compared to the honest pool with equal mining power, supporting our conclusions from Sec. V.

D. Experiment IV

Goal. The goal of this experiment was to investigate the transaction collision rate under the occurrence of greedy miners who selected transactions using the greedy strategy.

Methodology and Results. In contrast to the previous experiments, we considered three different values of block creation time (λ ∈ {10s, 20s, 60s}). We experimented with 10 miners, where the number of greedy miners G vs. the number of honest miners (i.e., 10 - G) was varied, and each held 10% of the total mining power. For all configurations, we computed the transaction collision rate (see Fig. 7b). We can see that the increase of G causes the increase in the transaction collision rate. Note that lower λ has a higher impact on the collision rate, and DAG protocols are designed with the intention to have small λ (i.e., even smaller than τ ). Consequently, the increased collision rate affected the overall throughput of the network (see Fig. 7c, which is complementary to Fig. 7b).

E. Experiments with Complex Topology

We conducted more than 500 experiments in complex topology with 7592 nodes in various configurations (such as different connectivity and positions of greedy miners in the topology). The generation of new transactions into mempools was made every 30 to 120 seconds and λ was set to 20 seconds. Since we know that τ > λ can cause a higher collision rate, we were interested in investigating this setting. Therefore, we distinguished two different ∂τ : 0.5s and 5s, which may be considered as the lower and upper boundary (the latter meets τ > λ since 25-35s > 20s).

The experiments with complex topology ran on the computation node with 20 cores and 128 GB of RAM, and they took 6 hours to complete on average. We emulated weakly and strongly connected miners by setting a different node degree – we utilized a node degree distribution from [32] and projected it into our network by setting the weakly connected edge and a highly connected core. We ensured the equal number of configurations with strongly and weekly connected greedy miners (which contributed to the spread in the results)

F. Experiment Complex-I

Goal. The goal of this experiment was to investigate the relative profit of one or more greedy miners w.r.t. the total mining power of the network. We aimed at repeating the experiments from Sec. VII-B and Sec. VII-C.

Methodology and Results. We compared two different scenarios. In the first one, we experimented with κ of a single greedy miner vs. the honest rest of the network, while in the second scenario, we assumed multiple greedy miners G = ∈ {1, . . . , 4} (each with κ = 10%); ∂τ was set to 5 seconds. We

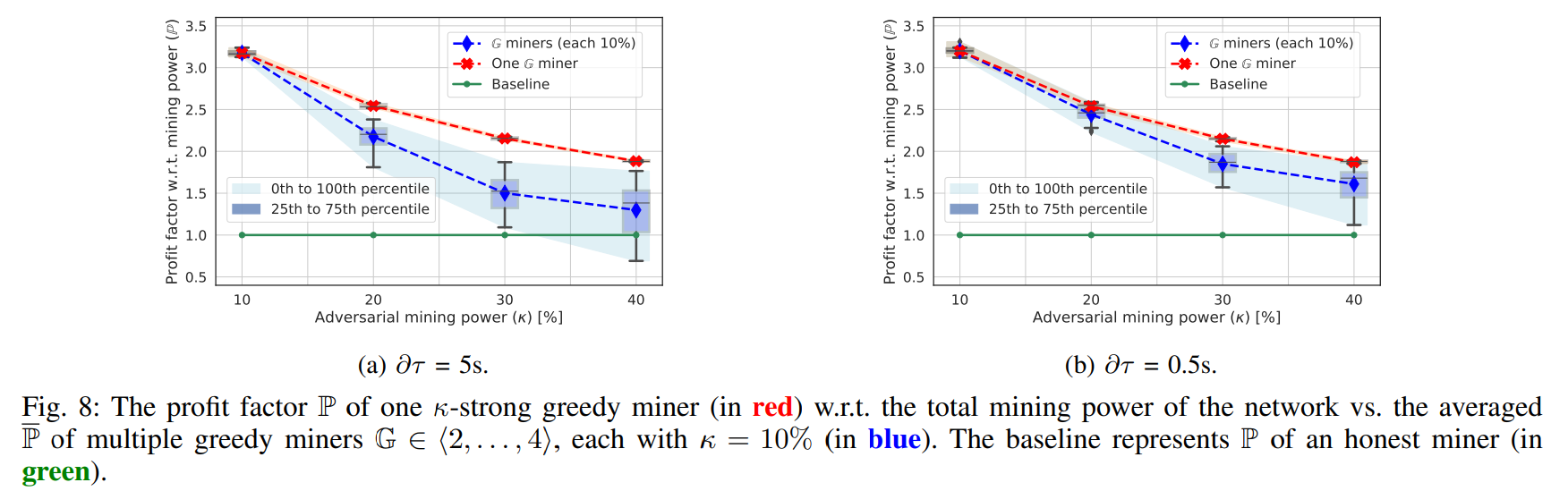
can see in Fig. 8a that a single miner is always more profitable than multiple miners, which might result in centralization by creating the greedy mining pool, as we outlined in Sec. VII-B. The difference in profitability between the cases of a single and multiple miners is also significant. If we compare these results to the simple topology, the single miner with κ = 10% can earn 33% of all profits in contrast to the simple topology where she can earn only 20% of all profits. This difference is not so significant with the higher κ. E.g., in the case of κ = 40%, a greedy miner on the complex topology can earn 75% of rewards, while in the simple network it is only 55%. This can be caused by the high τ , favoring greedy miners that can steal new “rich” transactions before they can be propagated in the blocks mined by honest miners.

We re-executed the experiment with ∂τ = 0.5s, emulating the lower boundary (i.e., real conditions). The results are depicted in Fig. 8b. We can see a similar trend as with ∂τ = 5 seconds but the absolute values differ, which confirms that incentive attacks on DAG-PROTOCOLS are feasible even with realistic settings, not necessarily requiring τ > λ.

G. Experiment Complex-II

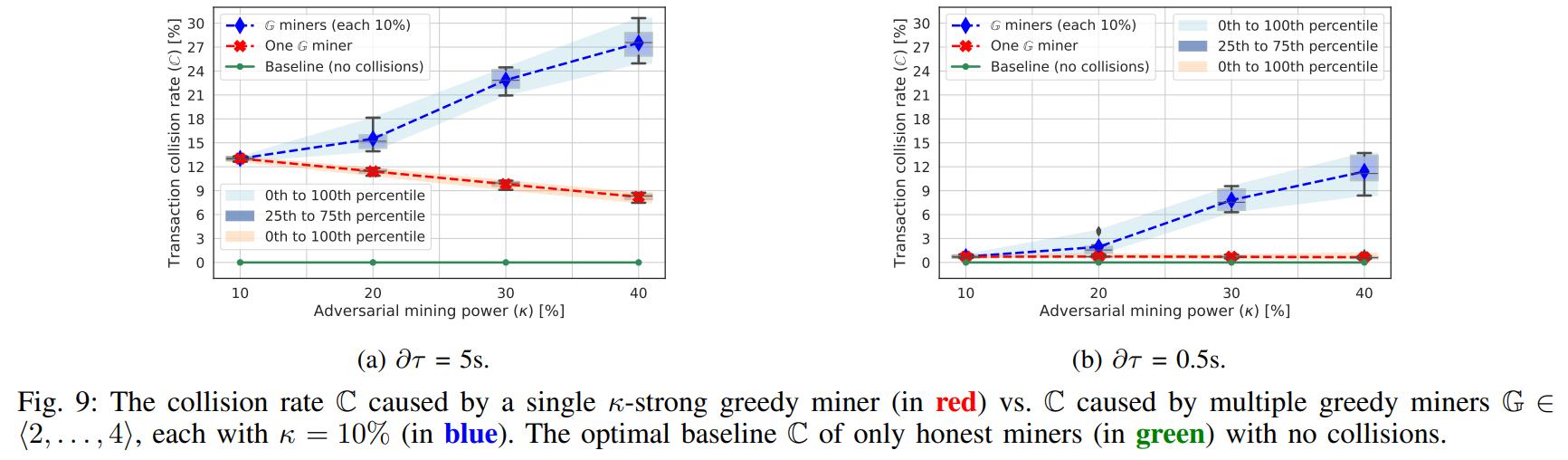
Goal. The goal of this experiment was to investigate the transaction collision rate C and the throughput of the network.

Methodology and Results. The methodology of the experiment is equivalent to Sec. VII-D. We used the setup with ∂τ adjusted to 5s and 0.5s, respectively (see Fig. 9). When comparing these two settings, as one can expect, C is significantly smaller if ∂τ = 0.5s than in the case of ∂τ = 5s. In the case of ∂τ = 5s, the miners have delayed information about already mined blocks (and their transactions), and thus updates of their mempools by deleting off transactions from already mined blocks are also delayed. Therefore, the impact of incentive attacks on collision rate is more significant when τ > λ (which is a common assumption in DAG-PROTOCOLs [44], [43], [46]). Another observation is that the lowest collision rate was achieved in the case of a single greedy miner, which decreases with increasing κ – the miner controls the larger portion of blocks and thus decreases collisions in them. However, this is not true with multiple such miners – they are competing and thus negatively affect the collision rate (and their profits). Therefore, they are incentivized in joining a mining pool to increase their profits (i.e., a single miner case).

H. Various Network Topologies

Goal. The goal of this experiment was to investigate the effect of different network topologies on the impact of incentive attacks to DAG-PROTOCOL.

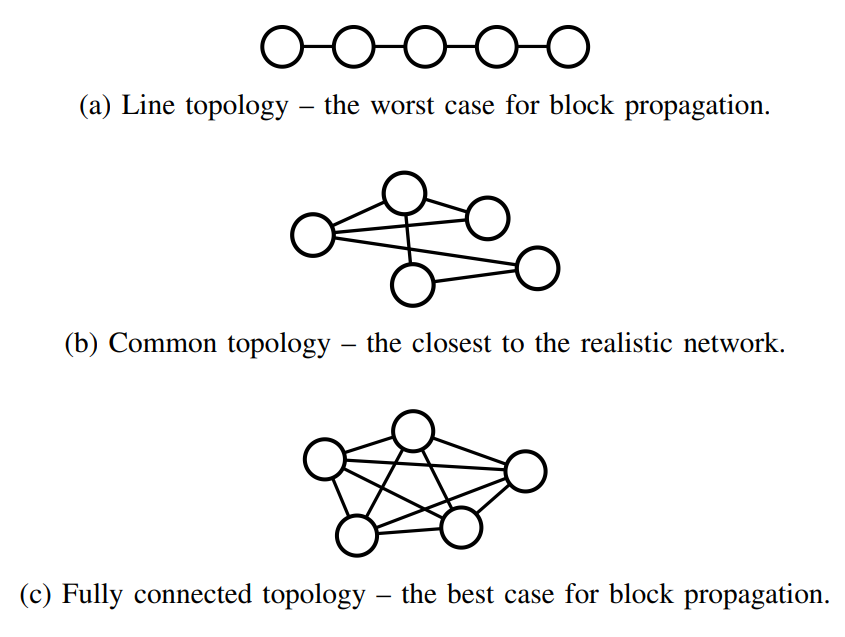
Methodology and Results. We experimented with three distinct network topologies, as shown in Fig. 10. Each network topology exhibited unique characteristics, which might not be realistic but enable us to investigate the effect of incentive attacks. The line topology represented the worst-case scenario, where the gossip between any two nodes was the slowest due to the presence of the only path for block propagation. The common topology represented the most realistic scenario with a strongly connected core and weakly connected edge. The fully connected topology represented the best case for the block propagation, where each message required only a single hop to be delivered. All topologies consisted of 7000 nodes, and the ∂τ was generated using the exponential distribution reflecting an approximate τ of 5 seconds, which was fitted using the data from [13]. Similar to the previous experiments,

a single greedy miner with κ ranging from 10% to 40% with a granularity of 10% mining power was present.

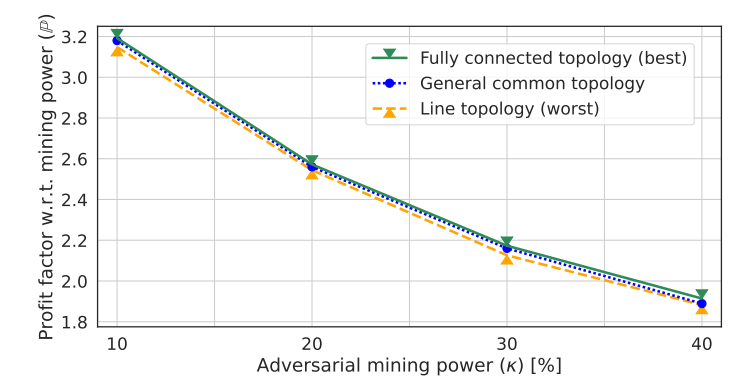
Results of this experiment are depicted in Fig. 11. We can observe that the network topology is almost an indifferent attribute. Nevertheless, there is a slight variability, which indicates that greedy miners are still favored. In sum, the decision to employ the greedy strategy is agnostic to network topology.

The primary simple rationale behind considering the fully connected topology as the best scenario is its capacity to offer a comprehensive and improved understanding (overall overview) of the network’s information dynamics, benefiting all participants involved. As a result, miners give precedence to transactions that have not yet been included in blocks throughout the entire network, leveraging their complete visibility of the information. This theoretical advantage allows for higher earnings and reduced collision rates. This phenomenon aligns with the principle that transactions yielding profits are rewarded exclusively to the first miner to include them in a block.