Table of Links
IX. Discussion and Future Work
IX. DISCUSSION AND FUTURE WORK
Centralization. In the scope of Experiment I (see Sec. VII-A), we demonstrated that the relative profit of greedy miners decreases as their number G increases. Therefore, greedy miners are incentivized to form a single mining pool, maximizing their relative profit. As a negative consequence, the decentralization of the blockchain network is impacted.
Throughout. In our simulations, we adjusted the parameters to focus on investigating potential issues related to decreased profits and general throughput (collisions), rather than maximizing the simulated protocol’s throughput. However, we argue that this had no impact on the results of our evaluation, and similar results can be achieved even with higher throughput (i.e., τ > λ).
Connectivity of Miners. In our experiments, we used γ = 1 and equally connected honest and greedy miners. However, in practice, greedy miners can be better connected since they want to include high-value transactions as the first ones, and thus profit even more. Assuming other γ than 1 can result only in lower profits of (potentially) weakly connected honest miners while it does reduce the profits of greedy miners who are incentivized to be strongly connected regardless of γ.
Future Work. We plan to experiment in detail with the methods enabling DAG-PROTOCOLS to be resilient to demonstrated attacks even in the context of Proof-of-Stake protocols. As
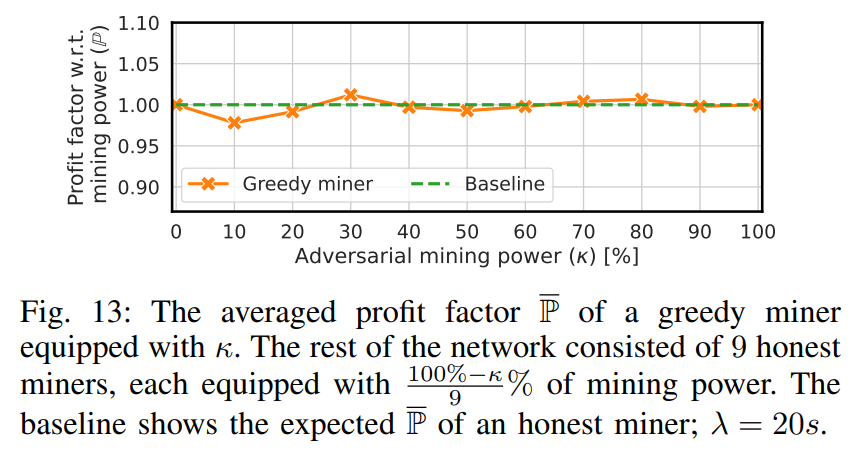
the next step in theoretical analysis, it would be interesting to examine the dynamic behavior of greedy miners who adapt their strategies (switching between multiple strategies) to the current conditions of the protocol. Last, we attributed a fee to the first miner who included a transaction in our simulations, but other schemes for distributing the fees among all miners could also be investigated. However, such schemes would not eliminate collisions (and thus decreased throughput), thereby enabling miners still to select transactions greedily due to varying fees.
Authors:
(1) Martin Peresıni, Brno University of Technology, Faculty of Information Technology ([email protected]);
(2) Ivan Homoliak, Brno University of Technology, Faculty of Information Technology ([email protected]);
(3) Federico Matteo Bencic, University of Zagreb, Faculty of Electrical Engineering and Computing ([email protected]);
(4) Martin Hruby, Brno University of Technology, Faculty of Information Technology ([email protected]);
(5) Kamil Malinka, Brno University of Technology, Faculty of Information Technology ([email protected]).
This paper is

