This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Bartosz Kusmierz, IOTA Foundation 10405 Berlin, Germany & Department of Theoretical Physics, Wroclaw University of Science and Technology, Poland [email protected];
(2) Roman Overko, IOTA Foundation 10405 Berlin, Germany [email protected].
Table of Links
II. RELATED WORK AND METHODOLOGY
One of the first works analyzing Bitcoin using network characteristics over time (as well as the wealth statistics and the temporal patterns of transactions) is presented in [6]. The authors showed that the wealth of top Bitcoin holders grows faster than the wealth of low balance accounts—this phenomenon is well known as preferential attachment, and it plays an essential role in the formation of the wealth distribution. Additionally, the Gini coefficients were also computed to measure wealth inequality. Analysis of the Bitcoin network from a perspective of mining pools can be found in [20], in which the authors studied how characteristics of mining pools such as computing power, hash rate, mining revenue, transaction collection strategies, and block size affect the security of the network, transaction delays, and fees. Their measurement results showed that more than 50% of the blocks were created by the top 5 mining pools, which may raise security and centralization concerns for the Bitcoin network.
The results of similar research to our work were presented in [11]. Specifically, the authors provided their analysis using three different metrics (Gini coefficient, Shannon entropy, and Nakamoto coefficient) and their evolution over time. It was found that the degree of decentralization in Bitcoin is higher and more volatile, while the degree of decentralization in Ethereum is smaller and more stable. Jensen et al. [4] analyzed decentralization of governance token distribution in four decentralized finance (DeFi) applications on the Ethereum blockchain using Gini and Nakamoto coefficients. Their results indicated that the token distributions for all four DeFi applications are characterized by high Gini coefficients. Similar methods were used in [10], where PoW and PoS-based cryptocurrencies were compared. The authors analyzed the decentralization of Bitcoin and Steem using Shannon entropy. However, their analysis was limited to only two cryptocurrencies and did not account for time changes in the distribution.
The authors of [22] constructed a growth model for a market capitalization of cryptocurrencies using Gibrat’s law. They also pointed out that crypto coins (which operate on their own independent DLT network) and crypto tokens (which operate on top of another coin platform) follow Zipf’s law for their capitalization. Although, the parameter of Zipf’s law is quantitatively different for coins and tokens.
A large part of research in such literature has been devoted to the analysis of the properties of cryptocurrencies networks from a graph perspective where each transaction is represented by a link in a graph of addresses [2], [9]–[11], [15], [16], [19]. For example, Lehnberg [9] aimed to determine whether the relationships between the users of ERC20 token networks and their valuations follow Metcalfe’s law. It was found that only two tokens of 50 seem to obey Metcalfe’s law, while the rest follow a linear or sub-linear law.
A. Data collection and cryptocurrency wallets
Many blockchain networks do not store balances associated with addresses; however, balances can be calculated from the sum of sent and received assets (i.e., coins or tokens) for each address. In this work, we use public blockchain datasets available on Google BigQuery[1]. Starting from the genesis block of a particular blockchain, we collected historical transaction/transfer data until January 16, 2022, inclusive. In the case of some ERC20 tokens, the first few weeks of the data had been skipped before the analysis due to the insufficient number of transactions. This early period could have been devoted to testing or marketing. Including these data could bring artifacts[2]
It is important to note that the data presented in this paper does not represent the wealth of individual cryptocurrency owners but rather the wealth distribution among the cryptocurrency wallets. Cryptocurrency wallets are not unique to a user, and one user can be in possession of multiple such wallets. The true identity of addresses owners is hard to establish and might be problematic even for entities that have access to the cryptocurrency exchanges’ data. Aware of these limits, we find the distribution of wealth in the richest cryptocurrency wallets to be still interesting as the basis of identity systems in PoS systems and DAOs are wallets (see section II-B).
B. Sample size N
In this paper, we analyze the properties of the empirical distribution function for the top N richest accounts. Such empirical distributions are discrete, and the value of the ith entry is the ratio of the i-th richest account balance to the sum of N richest account balances. We focus on a relatively small sample size N between 30—100. These numbers might seem arbitrary and small, especially in the face of thousands and tens of thousands of cryptocurrency users. However, this interval is interesting for applications in DPoS DLTs based on Byzantine Fault Tolerance (BFT) [1], [12], [17] consensus mechanisms.
In the most standard versions of BFT consensus mechanisms, the number of consensus participants is fixed, and their identities are known. Such systems are permissioned and not suitable for direct use in fully permissionless DLTs. However, an interesting modification to BFT design is used by a series of DPoS blockchains. These projects use an intermediary step between open and permissionless networks. Any user is allowed to set up a node and collect tokens, but only the most reliable nodes with the most stake contribute to the consensus directly. An illustration of the procedure of establishing consensus based on the fixed-size closed committee in open and permissionless systems is depicted in Fig. 1.
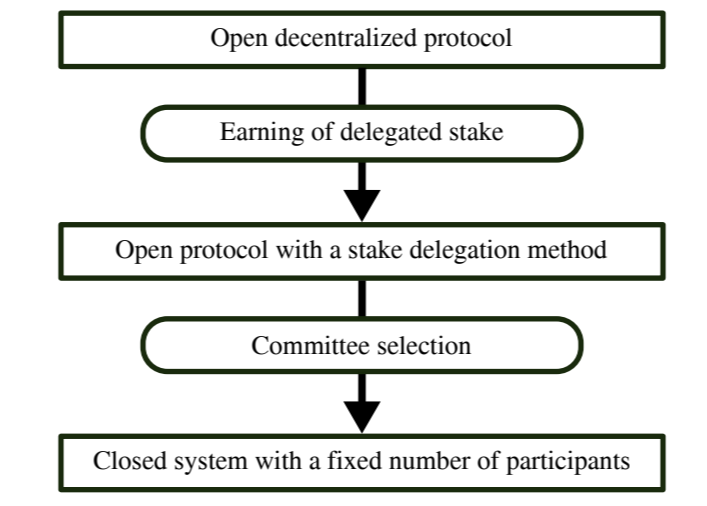
An example of a DPoS protocol is EOS[3] , in which blocks are produced by a committee of 21 validators who collectively sign the new blocks using an asynchronous version of the BFT consensus mechanism [8]. Committee members are selected and periodically rotated based on the amount of stake which was delegated to them by other network users. Other examples include Lisk[4] , which uses 101 nodes, and Internet Computer (ICP)[5] with the 101 nodes in the Neural Nervous System (ICP’s main blockchain). In theory, the size of block producing committee can be unbounded. However, in practice, the procedure of signing new blocks is limited by the bandwidth—the number of messages exchanged among the committee members grows like a square of its size. In the most practical applications, the block-producing committee has from 10 to 50 committee members. Some of the multiblockchain protocols might afford to use up to 100 nodes in some parts of their protocol; however, in these cases, the block production time suffers. These limits explain our interest in a relatively small interval of the sample size of N, namely 30— 100, which might be used to model the token distribution among block validators or improve the committee selection process.
C. Zipf ’s law
The Zipf’s distribution is a discrete distribution commonly found in physics and social sciences. It was empirically confirmed that the Zipf’s law describes a variety of effects in quantitative linguistics [23], the study of country and city population [3], and web sites references and other effects. Perhaps the most relevant for this paper are applications of the Zipf’s law in modeling the wealth in societies [5], and the distribution of token holders in various cryptocurrencies [6], [7], [10].

D. Centralization metrics
In this paper, we discuss multiple centralization metrics like Gini and Nakamoto coefficient. We want to stress again that analyzed sample size N is relatively small and can significantly influence values of these metrics due to the normalization factor H(s, N) in Eq. (1).

In the general case, the values of entropy are unbounded. However, when the number of available states N is fixed, then the entropy takes values from an interval [0, log(N)]. Maximal centralization corresponds to the entropy equal to zero, and decentralization grows with entropy.
2) Gini Coefficient: The Gini coefficient G is an inequality measure widely used in economics and social statistics:

which is the minimal number of actors who control more than half of the network resources. It was originally introduced to assess the feasibility of a 51% attack on the Bitcoin network.
[1] https://bigquery.cloud.google.com/dataset/bigquery-public-data
[2] For example, there were no token transfers for the first few weeks after the inception of the Tether (USDT) smart contract.
[3] https://eos.io/
[4] https://lisk.com/
[5] https://dfinity.org/

